Im Traveling Salesman Problem (TSP) sind gegeben: Eine Menge von Städten $S$, eine Start-Stadt $s_1 \in S$, und eine Kostenfunktion $cost: S {\times} S \rightarrow \mathbb{R}^+$. Diese gibt die Kosten an, um von einer Stadt zur nächsten zu reisen. Gesucht ist eine Reihung der Städte, so dass die Gesamtkosten minimiert werden.

Hinweis: Auch wenn diese Bedingung im Pseudo-Code in der Vorlesung nicht explizit war, gilt: Die Stadt $s_1$ ist als letzte der Route hinzuzufügen, so dass eine Rundreise entsteht.

• Skizzieren Sie in Pseudo-Code eine Routine backtrack_tsp(), die die Kosten der günstigsten Route mittels Backtracking berechnet. Orientieren Sie sich hierbei am Pseudo-Code aus der Vorlesung. Modellieren Sie zunächst die Zustände (was muss enthalten sein?). Wann können Sie die Suche als nicht-vielversprechend abbrechen?

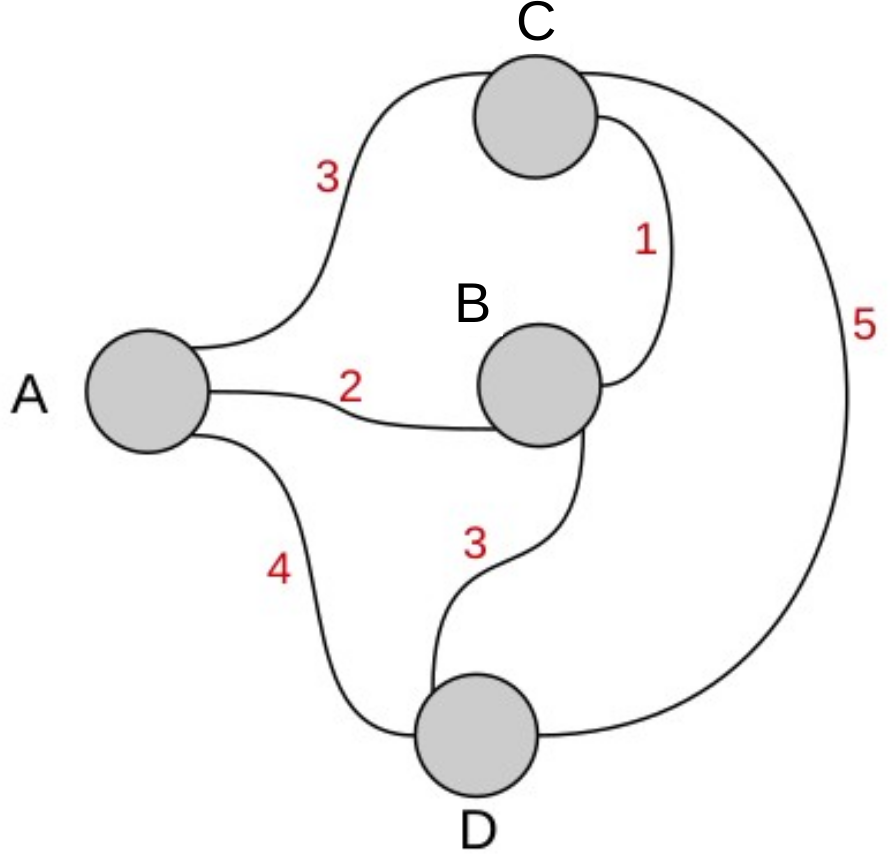
• In diesem Graph sei jeder Knoten eine Stadt. Die Route soll in Stadt A beginnen und enden. Die Kantenkosten sind jeweils in beide Richtungen zu verstehen, d.h. $cost(X,Y)=cost(Y,X)$. Skizzieren Sie den Verlauf Ihrer Backtracking-Suche in Baumform. Im Expansions-Schritt des Backtrackings expandieren Sie die Städte in alphabetischer Reihenfolge. Markieren Sie insbesondere, wo genau ihre Suche abbrechen kann weil keine Verbesserung mehr erzielt werden kann.