Implementieren Sie eine Methode solveBacktracking(), die per Backtracking nach einer Lösung sucht (d.h. einer Belegung, die die Formel erfüllt). Durchlaufen Sie hierfür die Variablen der Formel - zuerst $X_1$, dann $X_2$, usw., und probieren Sie für jede Variable zuerst die Belegung FALSE (=-1) und dann die Belegung TRUE (=1) aus. Brechen Sie die Suche ab sobald die Formel nicht mehr erfüllbar ist. Die folgende Abbildung illustriert den Verlauf der Backtracking-Suche in Baumform:
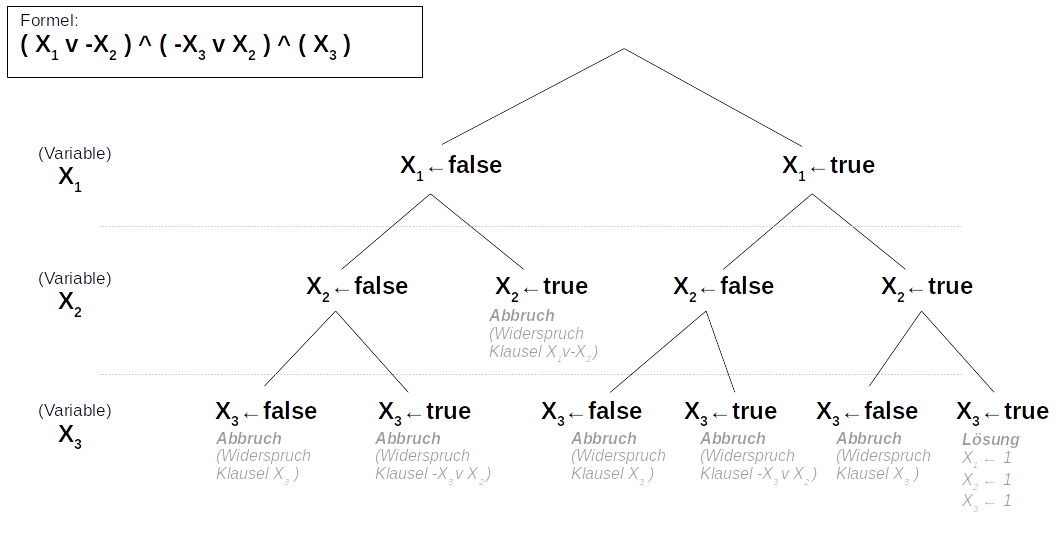
Hinweise:
- Sollte die Formel vorzeitig erfüllt sein, brechen Sie die Suche ab und geben die erfolgreiche Teilbelegung zurück. z.B. würde für die Formel (-X1 v -X2) vorzeitig die Belegung (-1,0) zurückgegeben - d.h. X2 bliebe "unbelegt".
- Falls Ihr Verfahren keine Lösung findet, soll die Ergebnis-Belegung ausschließlich Nullen enthalten.
- Gegebenenfalls sollten Sie Zustände klonen, bevor sie aus ihnen Folgezustände erzeugen.
- Wie immer ist es erlaubt, Hilfsmethoden hinzuzufügen.
- Ihre Implementierung soll die Eingabe-Formel nicht modifizieren.
package de.hsrm.ads;
public class LogicSolverBacktracking {
static boolean satisfies(short[] assignment, short[] clause) {
for (int i=0; i<clause.length; ++i)
if(assignment[i]*clause[i]==1)
return true;
return false;
}
// Bei Bedarf können Sie hierhin andere
// satisfies() / satisfiable() - Methoden
// aus LogicSolverGreedy kopieren.
static short[] solveBacktracking(short[][] formula) {
// FIXME
}
}

